Home > mathematics, Uncategorized > A Response to Terence Tao’s “An airport-inspired puzzle”

A Response to Terence Tao’s “An airport-inspired puzzle”

December 12, 2008 Leave a comment Go to comments

In Terence Tao’s latest post he poses three questions. Here are my solutions.

Suppose you are trying to get from one end A of a terminal to the other end B.  (For simplicity, assume the terminal is a one-dimensional line segment.)  Some portions of the terminal have moving walkways (in both directions); other portions do not.  Your walking speed is a constant v, but while on a walkway, it is boosted by the speed u of the walkway for a net speed of v+u.  (Obviously, one would only take those walkway that are going in the direction one wishes to travel in.)  Your objective is to get from A to B in the shortest time possible.

  1. Suppose you need to pause for some period of time, say to tie your shoe.  Is it more efficient to do so while on a walkway, or off the walkway?  Assume the period of time required is the same in both cases.
  2. Suppose you have a limited amount of energy available to run and increase your speed to a higher quantity v’ (or v’+u, if you are on a walkway).  Is it more efficient to run while on a walkway, or off the walkway?  Assume that the energy expenditure is the same in both cases.
  3. Do the answers to the above questions change if one takes into account the effects of special relativity?  (This is of course an academic question rather than a practical one.)

Source: Terence Tao, http://terrytao.wordpress.com/2008/12/09/an-airport-inspired-puzzle/

Q1.

After just thinking about it without any mathematics I was not to sure so I used a mathematical approach. The first thing I did was to draw a diagram,

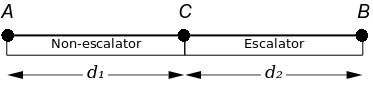diagram1Admittedly, I did simplify the problem in my diagram, however I am confident that this will not affect the final answer. (How do I prove this? I don’t know.) Along with this diagram I also had to define some things in terms of variables.

As shown in the diagram, A is the starting point, B is the ending point, C is an arbitrary point in between which separates the escalator section from the non-escalator sections.

Let,
t = time it takes to tie shoe lace
v = walking speed
u = escalator speed
T_{ac} = time it takes to get from A to C
T_{cb} = time it takes to get from C to B
T_{ab} = time it takes to get from A to B

We also know, speed = \frac {distance}{time}.

Now lets consider two scenarios. Scenario A, the person ties their shoe lace in the non-escalator section. Scenario B, the person ties their shoe lace in the escalator section.

Scenario A:

T_{ac}=T_{ab}+T_{bc}=\left (t+\frac{d_1}{v}\right )+\left (\frac{d_2}{v+u}\right )

Scenario B:

T_{ac}=T_{ab} + T_{bc}=\left ( \frac{d_1}{v}\right )+T_{bc}
Now let d_3 = \mbox{distance traveled in} d_2 \mbox{while the person is tieing their shoe lace.}\\\ \ =vt
\therefore \mbox{walking on escalator time for time } t_2 = \frac {d_2 - vt}{v+u}

I shall now make some reasonable assumptions (also formalising things a bit more),

All variables are real, and we shall assume that the person has time to tie their shoe lace while on the escalator. I.e. t \le \frac{d_2}{u}

I shall denote T_A to be T_{ac} from scenario A and T_B to be T_{ac} from scenario B. Now to see which is larger T_A or T_B we can examine the sign of T_A - T_B. If it is positive then T_A > T_B, if it is negative then T_A < T_B.

By some algebra T_A - T_B = \frac{vt}{v+u} and as v, u, t > 0,  T_A - T_B > 0. Hence T_B < T_A. Therefore it would be more efficient pause for a moment while on an escalator walkway.\

Q2.

I will take a similar approach for Q2, examining the two cases and then comparing the resultant time.

(I’ll re-edit the post when I get around to working out the solution)

Categories: mathematics, Uncategorized Tags:
  1. xbeta 善用佳软
    December 15, 2008 at 2:00 am
    Reply

    q1. pause on walkway.
    q2. run off walkway
    q3. the same

    q1:
    ——————————–
    3 people:
    　　A normal, B pause on walkway, C pause off walkway.

    A&B: on foot, then walkway.
    　　so A reach end first.
    At that time, B need more time to reach: vT/(u+v)

    A&C: walkway, then on foot.
    　　so A reach end first.
    At that time, C need more time to reach: vt/u

    So, B better than C.

    q2:
    ——————————–
    3 people:
    A normal, B run off walkway, C run on walkway.

    A&B: walkway, then on foot.
    So B reach end ealier.
    At that time, A need more time to reach: dTdV/v

    A&C: on foot, then walkway.
    So C reach end earlier.
    At that time, A need more time to reach: dTdV/(v+u)

    So, B is most ealier, better than C.

    q3:
    ——————————–
    advacned theory should not be conflict with obvious analization.

  1. No trackbacks yet.

I don't read comments anymore due to an increase in spam comments. If you want to get in touch please send me an email (see tianjara.net for details).